Measuring accuracy of XGBoost models#
(using stratified 5-fold cross validation, and a model with 10 features)
Plain English summary#
We have decided to simplify our model by using 10 independent features to predict which patients receive thrombolysis. This gives a good balance of performance (in terms of ROC AUC, achieving over 99% of what can be obtained with all of the 84 features) and model complexity.
There are many other ways in which to report model performance - in this notebook we will report on a range of these. The overall model accuracy is 84.7%, so between 8 and 9 out of 10 instances will have a correct prediction. The model is also well calibrated (for example, all of the patients that a model predicts 40% probability for, 40% of them did receive it).
Model and data#
XGBoost models were trained on stratified k-fold cross-validation data. The 10 features in the model are:
Arrival-to-scan time: Time from arrival at hospital to scan (mins)
Infarction: Stroke type (1 = infarction, 0 = haemorrhage)
Stroke severity: Stroke severity (NIHSS) on arrival
Precise onset time: Onset time type (1 = precise, 0 = best estimate)
Prior disability level: Disability level (modified Rankin Scale) before stroke
Stroke team: Stroke team attended
Use of AF anticoagulents: Use of atrial fibrillation anticoagulant (1 = Yes, 0 = No)
Onset-to-arrival time: Time from onset of stroke to arrival at hospital (mins)
Onset during sleep: Did stroke occur in sleep?
Age: Age (as middle of 5 year age bands)
And one target feature:
Thrombolysis: Receive thrombolysis (1 = Yes, 0 = No)
The 10 features included in the model (to predict whether a patient will receive thrombolysis) were chosen sequentially as having the single best improvement in model performance (using the ROC AUC). The stroke team feature is included as a one-hot encoded feature.
Aims#
Measure a range of accuracy scores (e.g. accuracy, sensitivity, specificity, F1, etc).
Plot Receiver Operator Characteristic Curve and measure AUC.
Identify cross-over point of sensitivity and specificity.
Compare predicted and observed thrombolysis use at each hospital.
Examine feature importances
Check model calibration (reliability)
Examine learning curves
Save individual patient predictions.
Observations#
Overall accuracy = 85.0%
Using nominal threshold (50% probability), specificity (89.4%) is greater than sensitivity (74.3%)
The model can achieve 83.9% sensitivity and specificity simultaneously
ROC AUC = 0.918
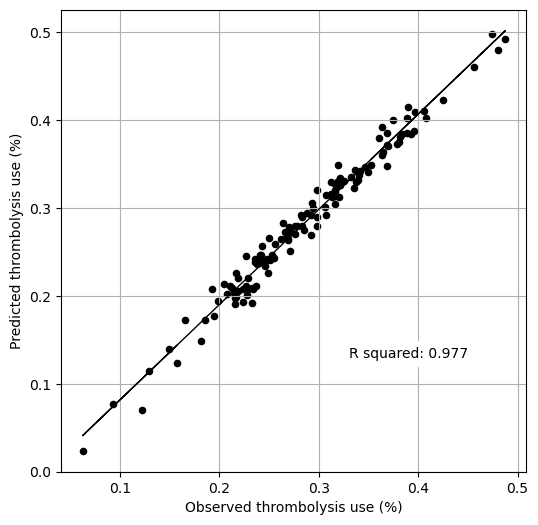
The model explains 97.7% of the variation of the observed thrombolysis use at each hospital.
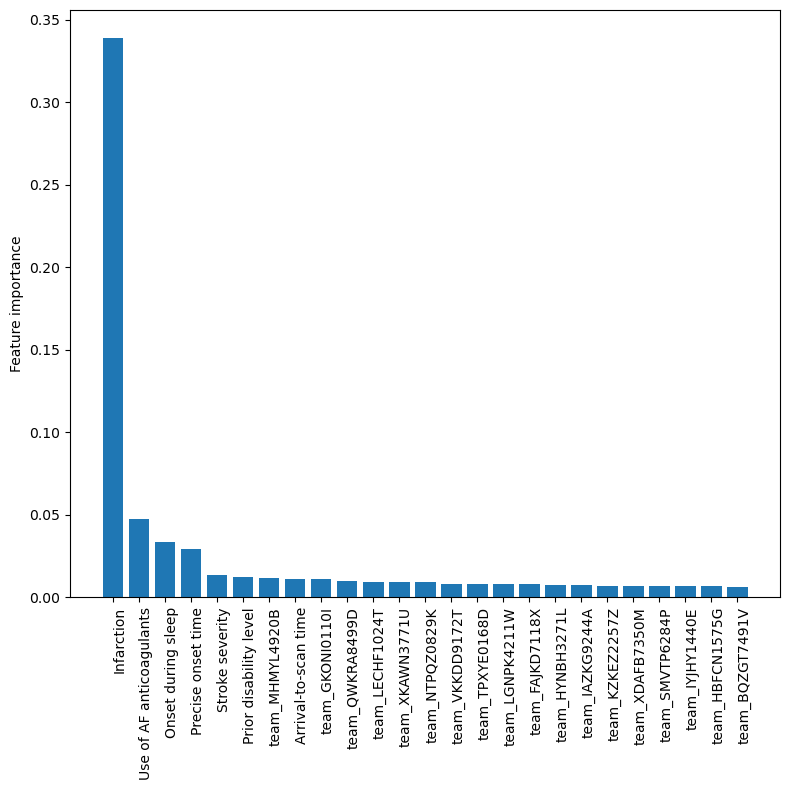
The top 5 features are: 1) stroke type, 2) use of AF anticoagulants, 3) onset during sleep, 4) onset time type, 5) stroke severity.
The model is well calibrated
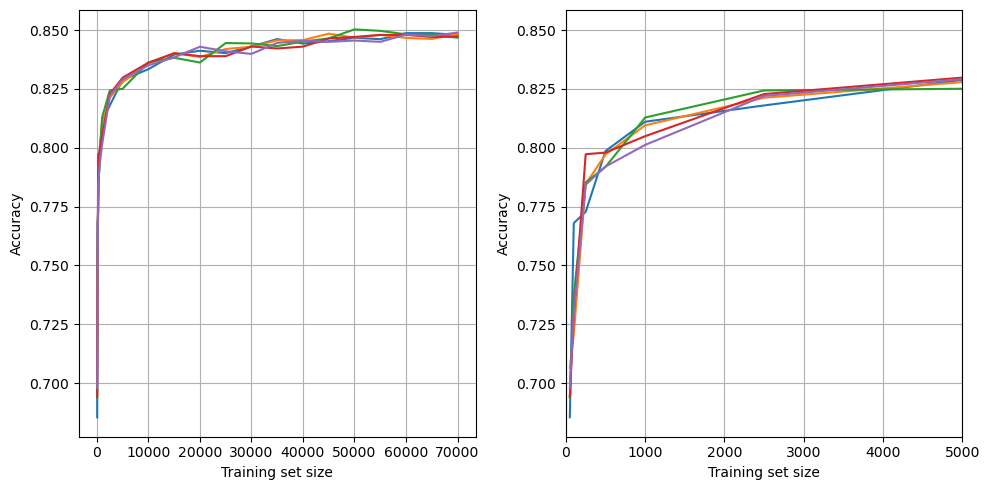
We have sufficient volume of data to train a model
Import libraries#
# Turn warnings off to keep notebook tidy
import warnings
warnings.filterwarnings("ignore")
import os
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import numpy as np
import pandas as pd
from xgboost import XGBClassifier
from sklearn.metrics import auc
from sklearn.metrics import roc_curve
from sklearn.linear_model import LinearRegression
import pickle
from sklearn import metrics
import json
Set filenames#
# Set up strings (describing the model) to use in filenames
number_of_features_to_use = 10
model_text = f'xgb_{number_of_features_to_use}_features'
notebook = '02'
Create output folders if needed#
path = './output'
if not os.path.exists(path):
os.makedirs(path)
path = './predictions'
if not os.path.exists(path):
os.makedirs(path)
path = './saved_models'
if not os.path.exists(path):
os.makedirs(path)
Read in JSON file#
Contains a dictionary for plain English feature names for the 10 features selected in the model. Use these as the column titles in the DataFrame.
with open("./output/01_feature_name_dict.json") as json_file:
feature_name_dict = json.load(json_file)
Load data#
Data has previously been split into 5 stratified k-fold splits.
data_loc = '../data/kfold_5fold/'
# Initialise empty lists
train_data_kfold, test_data_kfold = [], []
# Read in the names of the selected features for the model
key_features = pd.read_csv('./output/01_feature_selection.csv')
key_features = list(key_features['feature'])[:number_of_features_to_use]
# And add the target feature name: S2Thrombolysis
key_features.append("S2Thrombolysis")
# For each k-fold split
for k in range(5):
train = pd.read_csv(data_loc + 'train_{0}.csv'.format(k))
train = train[key_features]
train.rename(columns=feature_name_dict, inplace=True)
train_data_kfold.append(train)
test = pd.read_csv(data_loc + 'test_{0}.csv'.format(k))
test = test[key_features]
test.rename(columns=feature_name_dict, inplace=True)
test_data_kfold.append(test)
Functions#
Calculate accuracy measures#
def calculate_accuracy(observed, predicted):
"""
Calculates a range of accuracy scores from observed and predicted classes.
Takes two list or NumPy arrays (observed class values, and predicted class
values), and returns a dictionary of results.
1) observed positive rate: proportion of observed cases that are +ve
2) Predicted positive rate: proportion of predicted cases that are +ve
3) observed negative rate: proportion of observed cases that are -ve
4) Predicted negative rate: proportion of predicted cases that are -ve
5) accuracy: proportion of predicted results that are correct
6) precision: proportion of predicted +ve that are correct
7) recall: proportion of true +ve correctly identified
8) f1: harmonic mean of precision and recall
9) sensitivity: Same as recall
10) specificity: Proportion of true -ve identified:
11) positive likelihood: increased probability of true +ve if test +ve
12) negative likelihood: reduced probability of true +ve if test -ve
13) false positive rate: proportion of false +ves in true -ve patients
14) false negative rate: proportion of false -ves in true +ve patients
15) true positive rate: Same as recall
16) true negative rate: Same as specificity
17) positive predictive value: chance of true +ve if test +ve
18) negative predictive value: chance of true -ve if test -ve
"""
# Converts list to NumPy arrays
if type(observed) == list:
observed = np.array(observed)
if type(predicted) == list:
predicted = np.array(predicted)
# Calculate accuracy scores
observed_positives = observed == 1
observed_negatives = observed == 0
predicted_positives = predicted == 1
predicted_negatives = predicted == 0
true_positives = (predicted_positives == 1) & (observed_positives == 1)
false_positives = (predicted_positives == 1) & (observed_positives == 0)
true_negatives = (predicted_negatives == 1) & (observed_negatives == 1)
false_negatives = (predicted_negatives == 1) & (observed_negatives == 0)
accuracy = np.mean(predicted == observed)
precision = (np.sum(true_positives) /
(np.sum(true_positives) + np.sum(false_positives)))
recall = np.sum(true_positives) / np.sum(observed_positives)
sensitivity = recall
f1 = 2 * ((precision * recall) / (precision + recall))
specificity = np.sum(true_negatives) / np.sum(observed_negatives)
positive_likelihood = sensitivity / (1 - specificity)
negative_likelihood = (1 - sensitivity) / specificity
false_positive_rate = 1 - specificity
false_negative_rate = 1 - sensitivity
true_positive_rate = sensitivity
true_negative_rate = specificity
positive_predictive_value = (np.sum(true_positives) /
(np.sum(true_positives) + np.sum(false_positives)))
negative_predictive_value = (np.sum(true_negatives) /
(np.sum(true_negatives) + np.sum(false_negatives)))
# Create dictionary for results, and add results
results = dict()
results['observed_positive_rate'] = np.mean(observed_positives)
results['observed_negative_rate'] = np.mean(observed_negatives)
results['predicted_positive_rate'] = np.mean(predicted_positives)
results['predicted_negative_rate'] = np.mean(predicted_negatives)
results['accuracy'] = accuracy
results['precision'] = precision
results['recall'] = recall
results['f1'] = f1
results['sensitivity'] = sensitivity
results['specificity'] = specificity
results['positive_likelihood'] = positive_likelihood
results['negative_likelihood'] = negative_likelihood
results['false_positive_rate'] = false_positive_rate
results['false_negative_rate'] = false_negative_rate
results['true_positive_rate'] = true_positive_rate
results['true_negative_rate'] = true_negative_rate
results['positive_predictive_value'] = positive_predictive_value
results['negative_predictive_value'] = negative_predictive_value
return results
Fit XGBoost model#
Fit XGBoost model for each k-fold training/test split, and get feature importance values (a value per feature, per model from each k-fold split).
Save models.
# Fit models (True), or load models (False)
fit_models = True
# Set up lists to store k-fold fits
model_kfold = []
feature_importance_kfold = []
y_pred_proba_kfold = []
y_pred_class_kfold = []
X_train_kfold = []
X_test_kfold = []
y_train_kfold = []
y_test_kfold = []
accuracy_kfold = []
# Loop through k folds
for k in range(5):
# Get X and y
X_train = train_data_kfold[k].drop('Thrombolysis', axis=1)
X_test = test_data_kfold[k].drop('Thrombolysis', axis=1)
y_train = train_data_kfold[k]['Thrombolysis']
y_test = test_data_kfold[k]['Thrombolysis']
# One hot encode hospitals
X_train_hosp = pd.get_dummies(X_train['Stroke team'], prefix = 'team')
X_train = pd.concat([X_train, X_train_hosp], axis=1)
X_train.drop('Stroke team', axis=1, inplace=True)
X_test_hosp = pd.get_dummies(X_test['Stroke team'], prefix = 'team')
X_test = pd.concat([X_test, X_test_hosp], axis=1)
X_test.drop('Stroke team', axis=1, inplace=True)
# Store processed X and y
X_train_kfold.append(X_train)
X_test_kfold.append(X_test)
y_train_kfold.append(y_train)
y_test_kfold.append(y_test)
# Fit model
if fit_models:
# Define and Fit model
model = XGBClassifier(verbosity=0, seed=42, learning_rate=0.5)
model.fit(X_train, y_train)
model_kfold.append(model)
# Save using pickle
filename = (f'./saved_models/'
f'{notebook}_{model_text}_{k}.p')
with open(filename, 'wb') as filehandler:
pickle.dump(model, filehandler)
else:
# Load models
filename = (f'./saved_models/'
f'{notebook}_{model_text}_{k}.p')
with open(filename, 'rb') as filehandler:
model = pickle.load(filehandler)
model_kfold.append(model)
# Get and store predicted probability
y_pred_proba = model.predict_proba(X_test)[:, 1]
y_pred_proba_kfold.append(y_pred_proba)
# Get and store predicted class
y_pred_class = y_pred_proba >= 0.5
y_pred_class = np.array(y_pred_class) * 1.0
y_pred_class_kfold.append(y_pred_class)
# Get and store feature importances
feature_importance = model.feature_importances_
feature_importance_kfold.append(feature_importance)
# Print accuracy
accuracy_kfold.append(np.mean(y_pred_class == y_test))
print (
f'Run {k}, accuracy: {accuracy_kfold[k]:0.3f}')
Run 0, accuracy: 0.848
Run 1, accuracy: 0.853
Run 2, accuracy: 0.845
Run 3, accuracy: 0.854
Run 4, accuracy: 0.848
Results#
Accuracy measures#
# Set up list for results
results_kfold = []
# Loop through k fold predictions and get accuracy measures
for k in range(5):
results = calculate_accuracy(y_test_kfold[k], y_pred_class_kfold[k])
results_kfold.append(results)
# Put results in DataFrame
accuracy_results = pd.DataFrame(results_kfold).T
accuracy_results
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| observed_positive_rate | 0.295963 | 0.295737 | 0.295867 | 0.295529 | 0.295472 |
| observed_negative_rate | 0.704037 | 0.704263 | 0.704133 | 0.704471 | 0.704528 |
| predicted_positive_rate | 0.293879 | 0.293035 | 0.296824 | 0.292995 | 0.294008 |
| predicted_negative_rate | 0.706121 | 0.706965 | 0.703176 | 0.707005 | 0.705992 |
| accuracy | 0.848246 | 0.852582 | 0.845197 | 0.853981 | 0.847843 |
| precision | 0.745354 | 0.753075 | 0.737621 | 0.755141 | 0.743727 |
| recall | 0.740107 | 0.746192 | 0.740008 | 0.748666 | 0.740042 |
| f1 | 0.742721 | 0.749617 | 0.738812 | 0.751890 | 0.741880 |
| sensitivity | 0.740107 | 0.746192 | 0.740008 | 0.748666 | 0.740042 |
| specificity | 0.893706 | 0.897258 | 0.889395 | 0.898161 | 0.893054 |
| positive_likelihood | 6.962793 | 7.262741 | 6.690568 | 7.351502 | 6.919779 |
| negative_likelihood | 0.290804 | 0.282871 | 0.292325 | 0.279831 | 0.291089 |
| false_positive_rate | 0.106294 | 0.102742 | 0.110605 | 0.101839 | 0.106946 |
| false_negative_rate | 0.259893 | 0.253808 | 0.259992 | 0.251334 | 0.259958 |
| true_positive_rate | 0.740107 | 0.746192 | 0.740008 | 0.748666 | 0.740042 |
| true_negative_rate | 0.893706 | 0.897258 | 0.889395 | 0.898161 | 0.893054 |
| positive_predictive_value | 0.745354 | 0.753075 | 0.737621 | 0.755141 | 0.743727 |
| negative_predictive_value | 0.891069 | 0.893827 | 0.890606 | 0.894942 | 0.891202 |
accuracy_results.T.describe().T
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| observed_positive_rate | 5.0 | 0.295714 | 0.000211 | 0.295472 | 0.295529 | 0.295737 | 0.295867 | 0.295963 |
| observed_negative_rate | 5.0 | 0.704286 | 0.000211 | 0.704037 | 0.704133 | 0.704263 | 0.704471 | 0.704528 |
| predicted_positive_rate | 5.0 | 0.294148 | 0.001567 | 0.292995 | 0.293035 | 0.293879 | 0.294008 | 0.296824 |
| predicted_negative_rate | 5.0 | 0.705852 | 0.001567 | 0.703176 | 0.705992 | 0.706121 | 0.706965 | 0.707005 |
| accuracy | 5.0 | 0.849570 | 0.003619 | 0.845197 | 0.847843 | 0.848246 | 0.852582 | 0.853981 |
| precision | 5.0 | 0.746984 | 0.007151 | 0.737621 | 0.743727 | 0.745354 | 0.753075 | 0.755141 |
| recall | 5.0 | 0.743003 | 0.004134 | 0.740008 | 0.740042 | 0.740107 | 0.746192 | 0.748666 |
| f1 | 5.0 | 0.744984 | 0.005523 | 0.738812 | 0.741880 | 0.742721 | 0.749617 | 0.751890 |
| sensitivity | 5.0 | 0.743003 | 0.004134 | 0.740008 | 0.740042 | 0.740107 | 0.746192 | 0.748666 |
| specificity | 5.0 | 0.894315 | 0.003522 | 0.889395 | 0.893054 | 0.893706 | 0.897258 | 0.898161 |
| positive_likelihood | 5.0 | 7.037477 | 0.268855 | 6.690568 | 6.919779 | 6.962793 | 7.262741 | 7.351502 |
| negative_likelihood | 5.0 | 0.287384 | 0.005640 | 0.279831 | 0.282871 | 0.290804 | 0.291089 | 0.292325 |
| false_positive_rate | 5.0 | 0.105685 | 0.003522 | 0.101839 | 0.102742 | 0.106294 | 0.106946 | 0.110605 |
| false_negative_rate | 5.0 | 0.256997 | 0.004134 | 0.251334 | 0.253808 | 0.259893 | 0.259958 | 0.259992 |
| true_positive_rate | 5.0 | 0.743003 | 0.004134 | 0.740008 | 0.740042 | 0.740107 | 0.746192 | 0.748666 |
| true_negative_rate | 5.0 | 0.894315 | 0.003522 | 0.889395 | 0.893054 | 0.893706 | 0.897258 | 0.898161 |
| positive_predictive_value | 5.0 | 0.746984 | 0.007151 | 0.737621 | 0.743727 | 0.745354 | 0.753075 | 0.755141 |
| negative_predictive_value | 5.0 | 0.892329 | 0.001930 | 0.890606 | 0.891069 | 0.891202 | 0.893827 | 0.894942 |
Receiver Operator Characteristic and Sensitivity-Specificity Curves#
Receiver Operator Characteristic Curve:
# Set up lists for results
fpr_kfold = [] # false positive rate
tpr_kfold = [] # true positive rate
thresholds_kfold = [] # threshold applied
auc_kfold = [] # area under curve
# Loop through k fold predictions and get ROC results
for k in range(5):
fpr, tpr, thresholds = roc_curve(y_test_kfold[k], y_pred_proba_kfold[k])
roc_auc = auc(fpr, tpr)
fpr_kfold.append(fpr)
tpr_kfold.append(tpr)
thresholds_kfold.append(thresholds)
auc_kfold.append(roc_auc)
# Show mean area under curve
mean_auc = np.mean(auc_kfold)
sd_auc = np.std(auc_kfold)
print (f'\nMean AUC: {mean_auc:0.4f}')
print (f'SD AUC: {sd_auc:0.4f}')
Mean AUC: 0.9180
SD AUC: 0.0025
Calculate data for sensitivity-specificity curve:
# Initialise lists
sensitivity_kfold = []
specificity_kfold = []
# Loop through k folds
for k in range(5):
# Get classification probabilities for k-fold replicate
observed = y_test_kfold[k]
proba = y_pred_proba_kfold[k]
# Set up list for accuracy measures
sensitivity = []
specificity = []
# Loop through increments in probability of survival
thresholds = np.arange(0.0, 1.01, 0.01)
for cutoff in thresholds: # loop 0 --> 1 on steps of 0.1
# Get classificiation using cutoff
predicted_class = proba >= cutoff
predicted_class = predicted_class * 1.0
# Call accuracy measures function
accuracy = calculate_accuracy(observed, predicted_class)
# Add accuracy scores to lists
sensitivity.append(accuracy['sensitivity'])
specificity.append(accuracy['specificity'])
# Add replicate to lists
sensitivity_kfold.append(sensitivity)
specificity_kfold.append(specificity)
Create a combined plot: ROC and sensitivity-specificity
fig = plt.figure(figsize=(10,5))
# Plot ROC
ax1 = fig.add_subplot(121)
for k in range(5):
ax1.plot(fpr_kfold[k], tpr_kfold[k], color='orange')
ax1.plot([0, 1], [0, 1], color='darkblue', linestyle='--')
ax1.set_xlabel('False Positive Rate')
ax1.set_ylabel('True Positive Rate')
ax1.set_title('Receiver Operator Characteristic Curve')
text = f'Mean AUC: {mean_auc:.3f}'
ax1.text(0.64,0.07, text,
bbox=dict(facecolor='white', edgecolor='black'))
plt.grid(True)
# Plot sensitivity-specificity
ax2 = fig.add_subplot(122)
for k in range(5):
ax2.plot(sensitivity_kfold[k], specificity_kfold[k])
ax2.set_xlabel('Sensitivity')
ax2.set_ylabel('Specificity')
ax2.set_title('Sensitivity-Specificity Curve')
plt.grid(True)
plt.tight_layout(pad=2)
plt.savefig(f'./output/{notebook}_{model_text}_roc_sens_spec.jpg', dpi=300)
plt.show()
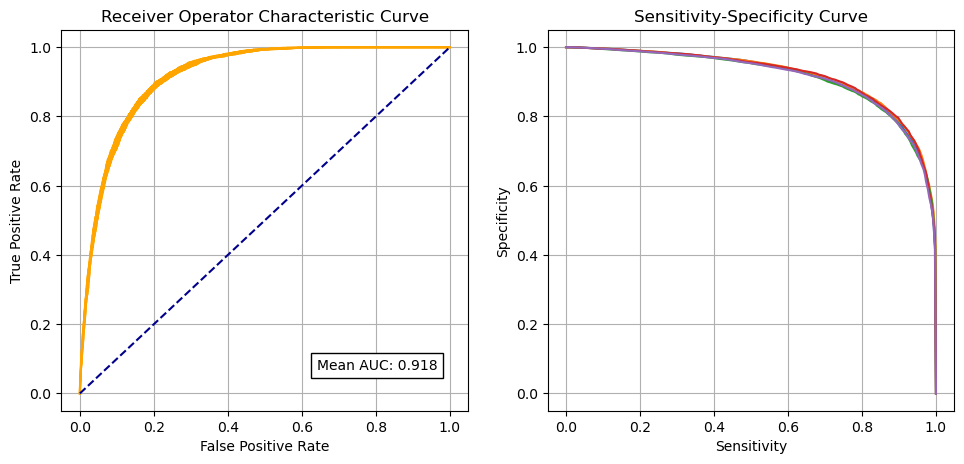
Identify cross-over point on sensitivity-specificity curve#
Adjusting the classification threshold allows us to balance sensitivity (the proportion of patients receiving thrombolysis correctly identified) and specificity (the proportion of patients not receiving thrombolysis correctly identified). An increase in sensitivity causes a loss in specificity (and vice versa). Here we identify the pint where specificity and sensitivity hold the same value.
def get_intersect(a1, a2, b1, b2):
"""
Returns the point of intersection of the lines passing through a2,a1 and
b2,b1.
a1: [x, y] a point on the first line
a2: [x, y] another point on the first line
b1: [x, y] a point on the second line
b2: [x, y] another point on the second line
"""
s = np.vstack([a1,a2,b1,b2]) # s for stacked
h = np.hstack((s, np.ones((4, 1)))) # h for homogeneous
l1 = np.cross(h[0], h[1]) # get first line
l2 = np.cross(h[2], h[3]) # get second line
x, y, z = np.cross(l1, l2) # point of intersection
if z == 0: # lines are parallel
return (float('inf'), float('inf'))
return (x/z, y/z)
intersections = []
for k in range(5):
sens = np.array(sensitivity_kfold[k])
spec = np.array(specificity_kfold[k])
df = pd.DataFrame()
df['sensitivity'] = sens
df['specificity'] = spec
df['spec greater sens'] = spec > sens
# find last index for senitivity being greater than specificity
mask = df['spec greater sens'] == False
last_id_sens_greater_spec = np.max(df[mask].index)
locs = [last_id_sens_greater_spec, last_id_sens_greater_spec + 1]
points = df.iloc[locs][['sensitivity', 'specificity']]
# Get intersetction with line of x=y
a1 = list(points.iloc[0].values)
a2 = list(points.iloc[1].values)
b1 = [0, 0]
b2 = [1, 1]
intersections.append(get_intersect(a1, a2, b1, b2)[0])
mean_intersection = np.mean(intersections)
sd_intersection = np.std(intersections)
print (f'\nMean intersection: {mean_intersection:0.4f}')
print (f'SD intersection: {sd_intersection:0.4f}')
Mean intersection: 0.8393
SD intersection: 0.0027
Collate and save results#
hospital_results = []
kfold_results = []
observed_results = []
prob_results = []
predicted_results = []
for k in range(5):
hospital_results.extend(list(test_data_kfold[k]['Stroke team']))
kfold_results.extend(list(np.repeat(k, len(test_data_kfold[k]))))
observed_results.extend(list(y_test_kfold[k]))
prob_results.extend(list(y_pred_proba_kfold[k]))
predicted_results.extend(list(y_pred_class_kfold[k]))
model_predictions = pd.DataFrame()
model_predictions['hospital'] = hospital_results
model_predictions['observed'] = np.array(observed_results) * 1.0
model_predictions['prob'] = prob_results
model_predictions['predicted'] = predicted_results
model_predictions['k_fold'] = kfold_results
model_predictions['correct'] = (
model_predictions['observed'] == model_predictions['predicted'])
# Save
filename = f'./predictions/02_{model_text}_predictions.csv'
model_predictions.to_csv(filename, index=False)
# Save combined test set
combined_test_set = pd.concat(test_data_kfold, axis=0)
combined_test_set.reset_index(inplace=True); del combined_test_set['index']
combined_test_set.to_csv(f'./predictions/'
f'{notebook}_{model_text}_combined_test_features.csv',
index=False)
Compare predicted and actual thrombolysis rates#
We compare the actual and predicted thrombolysis rates, taken from collating the five test sets (in k-fold validation all instances are in one, and only one, test set).
mean_results_by_hosp = model_predictions.groupby('hospital').mean()
Get r-square of predicted thrombolysis rate.
x_comparision = np.array(mean_results_by_hosp['observed']).reshape(-1, 1)
y_comparision = np.array(mean_results_by_hosp['predicted']).reshape(-1, 1)
slr = LinearRegression()
slr.fit(x_comparision, y_comparision)
y_pred = slr.predict(x_comparision)
r_square = metrics.r2_score(y_comparision, y_pred)
print(f'R squared {r_square:0.3f}')
R squared 0.977
fig = plt.figure(figsize=(6,6))
ax1 = fig.add_subplot(111)
ax1.scatter(x_comparision,
y_comparision, c='k', s=20)
plt.plot (x_comparision, slr.predict(x_comparision), color = 'k', linewidth=1)
text = f'R squared: {r_square:.3f}'
ax1.text(0.33,0.13, text,
bbox=dict(facecolor='white', edgecolor='white'))
ax1.set_xlabel('Observed thrombolysis use (%)')
ax1.set_ylabel('Predicted thrombolysis use (%)')
plt.grid()
plt.savefig(f'output/{notebook}_{model_text}_observed_predicted_rates.jpg',
dpi=300)
plt.show()
Show difference between predicted and observed.
diff = mean_results_by_hosp['observed'] - mean_results_by_hosp['predicted']
diff.describe()
count 132.000000
mean 0.002797
std 0.014317
min -0.029851
25% -0.005546
50% 0.001765
75% 0.010494
max 0.051829
dtype: float64
Show absolute difference between predicted and observed.
abs_diff = np.abs(mean_results_by_hosp['observed'] - mean_results_by_hosp['predicted'])
abs_diff.describe()
count 132.000000
mean 0.010846
std 0.009713
min 0.000000
25% 0.003808
50% 0.007745
75% 0.016260
max 0.051829
dtype: float64
Feature Importances#
Get XGBoost feature importances (average across k-fold results)
# Feature names
feature_names = X_test_kfold[0].columns.values
# Get average feature importance from k-fold
importances = np.array(feature_importance_kfold).mean(axis = 0)
# Store in DataFrame
feature_importance_df = pd.DataFrame(data = importances, index=feature_names)
feature_importance_df.columns = ['importance']
# Sort by importance (weight)
feature_importance_df.sort_values(by='importance',
ascending=False, inplace=True)
# Save
feature_importance_df.to_csv(f'output/'
f'{notebook}_{model_text}_feature_importance.csv')
# Display top 25
feature_importance_df.head(25)
| importance | |
|---|---|
| Infarction | 0.338992 |
| Use of AF anticoagulants | 0.047162 |
| Onset during sleep | 0.033632 |
| Precise onset time | 0.029524 |
| Stroke severity | 0.013365 |
| Prior disability level | 0.012285 |
| team_MHMYL4920B | 0.011416 |
| Arrival-to-scan time | 0.011349 |
| team_GKONI0110I | 0.011299 |
| team_QWKRA8499D | 0.009606 |
| team_LECHF1024T | 0.009506 |
| team_XKAWN3771U | 0.009336 |
| team_NTPQZ0829K | 0.009190 |
| team_VKKDD9172T | 0.008111 |
| team_TPXYE0168D | 0.007998 |
| team_LGNPK4211W | 0.007902 |
| team_FAJKD7118X | 0.007834 |
| team_HYNBH3271L | 0.007421 |
| team_IAZKG9244A | 0.007191 |
| team_KZKEZ2257Z | 0.007098 |
| team_XDAFB7350M | 0.007032 |
| team_SMVTP6284P | 0.007002 |
| team_IYJHY1440E | 0.006833 |
| team_HBFCN1575G | 0.006648 |
| team_BQZGT7491V | 0.006371 |
Create a bar chart for the XGBoost feature importance values
# Set up figure
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)
# Get labels and values
labels = feature_importance_df.index.values[0:25]
pos = np.arange(len(labels))
val = feature_importance_df['importance'].values[0:25]
# Plot
ax.bar(pos, val)
ax.set_ylabel('Feature importance')
ax.set_xticks(np.arange(len(labels)))
ax.set_xticklabels(labels)
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=90, ha="right",
rotation_mode="anchor")
plt.tight_layout()
plt.savefig(f'output/{notebook}_{model_text}_feature_weights_bar.jpg', dpi=300)
plt.show()
Calibration and assessment of accuracy when model has high confidence#
# Collate results in Dataframe
reliability_collated = pd.DataFrame()
# Loop through k fold predictions
for k in range(5):
# Get observed class and predicted probability
observed = y_test_kfold[k]
probability = y_pred_proba_kfold[k]
# Bin data with numpy digitize (this will assign a bin to each case)
step = 0.10
bins = np.arange(step, 1+step, step)
digitized = np.digitize(probability, bins)
# Put single fold data in DataFrame
reliability = pd.DataFrame()
reliability['bin'] = digitized
reliability['probability'] = probability
reliability['observed'] = observed
classification = 1 * (probability > 0.5 )
reliability['correct'] = observed == classification
reliability['count'] = 1
# Summarise data by bin in new dataframe
reliability_summary = pd.DataFrame()
# Add bins and k-fold to summary
reliability_summary['bin'] = bins
reliability_summary['k-fold'] = k
# Calculate mean of predicted probability of thrombolysis in each bin
reliability_summary['confidence'] = \
reliability.groupby('bin').mean()['probability']
# Calculate the proportion of patients who receive thrombolysis
reliability_summary['fraction_positive'] = \
reliability.groupby('bin').mean()['observed']
# Calculate proportion correct in each bin
reliability_summary['fraction_correct'] = \
reliability.groupby('bin').mean()['correct']
# Calculate fraction of results in each bin
reliability_summary['fraction_results'] = \
reliability.groupby('bin').sum()['count'] / reliability.shape[0]
# Add k-fold results to DatafRame collation
reliability_collated = reliability_collated.append(reliability_summary)
# Get mean results
reliability_summary = reliability_collated.groupby('bin').mean()
reliability_summary.drop('k-fold', axis=1, inplace=True)
reliability_summary
| confidence | fraction_positive | fraction_correct | fraction_results | |
|---|---|---|---|---|
| bin | ||||
| 0.1 | 0.017739 | 0.022712 | 0.977288 | 0.480111 |
| 0.2 | 0.146044 | 0.174410 | 0.825590 | 0.082023 |
| 0.3 | 0.247906 | 0.270556 | 0.729444 | 0.055681 |
| 0.4 | 0.348492 | 0.370611 | 0.629389 | 0.045410 |
| 0.5 | 0.449804 | 0.443144 | 0.556856 | 0.042628 |
| 0.6 | 0.550810 | 0.546112 | 0.546112 | 0.041997 |
| 0.7 | 0.651586 | 0.642829 | 0.642829 | 0.049340 |
| 0.8 | 0.752894 | 0.736410 | 0.736410 | 0.064983 |
| 0.9 | 0.851912 | 0.827386 | 0.827386 | 0.089107 |
| 1.0 | 0.932317 | 0.892702 | 0.892702 | 0.048721 |
Plot results:
fig = plt.figure(figsize=(10,5))
# Plot predicted prob vs fraction psotive
ax1 = fig.add_subplot(1,2,1)
# Loop through k-fold reliability results
for k in range(5):
mask = reliability_collated['k-fold'] == k
result_kfold = reliability_collated[mask]
x = result_kfold['confidence']
y = result_kfold['fraction_positive']
ax1.plot(x,y, color='orange')
# Add 1:1 line
ax1.plot([0,1],[0,1], color='k', linestyle ='--')
# Refine plot
ax1.set_xlabel('Model probability')
ax1.set_ylabel('Fraction positive')
ax1.set_xlim(0, 1)
ax1.set_ylim(0, 1)
# Plot accuracy vs probability
ax2 = fig.add_subplot(1,2,2)
# Loop through k-fold reliability results
for k in range(5):
mask = reliability_collated['k-fold'] == k
result_kfold = reliability_collated[mask]
x = result_kfold['confidence']
y = result_kfold['fraction_correct']
ax2.plot(x,y, color='orange')
# Refine plot
ax2.set_xlabel('Model probability')
ax2.set_ylabel('Fraction correct')
ax2.set_xlim(0, 1)
ax2.set_ylim(0, 1)
# instantiate a second axes that shares the same x-axis
ax3 = ax2.twinx()
for k in range(5):
mask = reliability_collated['k-fold'] == k
result_kfold = reliability_collated[mask]
x = result_kfold['confidence']
y = result_kfold['fraction_results']
ax3.plot(x,y, color='blue')
ax3.set_xlim(0, 1)
ax3.set_ylim(0, 0.5)
ax3.set_ylabel('Fraction of samples')
custom_lines = [Line2D([0], [0], color='orange', alpha=0.6, lw=2),
Line2D([0], [0], color='blue', alpha = 0.6,lw=2)]
ax1.grid()
ax2.grid()
plt.legend(custom_lines, ['Fraction correct', 'Fraction of samples'],
loc='upper center')
plt.tight_layout(pad=2)
plt.savefig(f'./output/{notebook}_{model_text}_reliability.jpg', dpi=300)
plt.show()
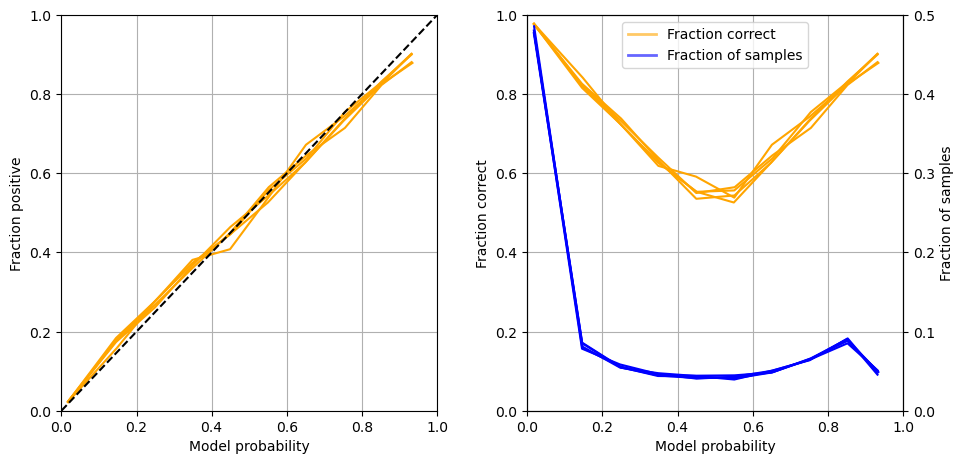
Get accuracy of model when model is at least 80% confident
bins = [0.1, 0.2, 0.9, 1.0]
acc = reliability_summary.loc[bins].mean()['fraction_correct']
frac = reliability_summary.loc[bins].sum()['fraction_results']
print ('For samples with at least 80% confidence:')
print (f'Proportion of all samples: {frac:0.3f}')
print (f'Accuracy: {acc:0.3f}')
For samples with at least 80% confidence:
Proportion of all samples: 0.700
Accuracy: 0.881
Check for predicted thrombolysis in test set#
mask = combined_test_set['Infarction'] == 0
haemorrhagic_test = model_predictions['predicted'][mask]
count = len(haemorrhagic_test)
pos = haemorrhagic_test.sum()
print (f'{pos:.0f} predicted thrombolysis out of {count} haemorrhagic strokes')
0 predicted thrombolysis out of 13243 haemorrhagic strokes
Learning curve#
Examine the relationship between training data size and accuracy.
Plot learning curve
# Set up list to collect results
results_training_size = []
results_accuracy = []
results_all_accuracy = []
# Get maximum training size (number of training records)
max_training_size = train_data_kfold[0].shape[0]
# Get X and y for test (from first k-fold split)
X_test = X_test_kfold[0]
y_test = y_test_kfold[0]
# Construct training sizes (values closer at lower end)
train_sizes = [50, 100, 250, 500, 1000, 2500]
for i in range (5000, max_training_size, 5000):
train_sizes.append(i)
# Loop through training sizes
for train_size in train_sizes:
# Record accuracy across k-fold replicates
replicate_accuracy = []
for replicate in range(5):
# Get X and y for train (from first k-fold split)
X_train = X_train_kfold[0]
y_train = y_train_kfold[0]
# Sample from training data
X_train = X_train.sample(n=train_size)
y_train = y_train.loc[X_train.index.values]
# Define model
model = XGBClassifier(verbosity = 0, seed=42, learning_rate=0.5)
# Fit model
model.fit(X_train, y_train)
# Predict test set
y_pred_test = model.predict(X_test)
# Get accuracy and record results
accuracy = np.mean(y_pred_test == y_test)
replicate_accuracy.append(accuracy)
results_all_accuracy.append(accuracy)
# Store mean accuracy across the k-fold splits
results_accuracy.append(np.mean(replicate_accuracy))
results_training_size.append(train_size)
accuracy_kfold = np.array(results_all_accuracy).reshape(len(train_sizes), 5)
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(121)
for k in range(5):
ax1.plot(results_training_size, accuracy_kfold[:, k])
ax1.set_xlabel('Training set size')
ax1.set_ylabel('Accuracy')
ax1.grid()
# Focus on first 5000
ax2 = fig.add_subplot(122)
for k in range(5):
ax2.plot(results_training_size, accuracy_kfold[:, k])
ax2.set_xlabel('Training set size')
ax2.set_ylabel('Accuracy')
ax2.set_xlim(0, 5000)
ax2.grid()
plt.tight_layout()
plt.savefig(f'./output/{notebook}_{model_text}_learning_curve.jpg', dpi=300)
plt.show()