Testing of SAMueL-1 synthetic data: descriptive statistics

In this notebook we comapre the descriptive statistics for synthetic and real data. Synthetic data is generated from each five k-fold training sets, and here we compare the synthetic to the original data.

We usew thhe ‘double’ smytnhetic data - two rounds of SMOTE.

Load packages

# Turn warnings off to keep notebook tidy
import warnings
warnings.filterwarnings("ignore")

import os
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import numpy as np
import pandas as pd

Load data

data_loc = './../data/sam_1/kfold_5fold/'

train_data, test_data, synthetic_data = [], [], []

for i in range(5):
    train_data.append(pd.read_csv(f'{data_loc}train_{i}.csv'))
    test_data.append(pd.read_csv(f'{data_loc}test_{i}.csv'))
    #synthetic_data.append(pd.read_csv(f'{data_loc}synth_train_{i}.csv'))
    synthetic_data.append(pd.read_csv(f'{data_loc}synthetic_double_{i}.csv'))

descriptive_stats_all_runs = []

for run in range(5):
    
    synth_df = synthetic_data[run].drop('StrokeTeam', axis=1)
    original_data = train_data[run].drop('StrokeTeam', axis=1)
        
  
    descriptive_stats = pd.DataFrame()

    descriptive_stats['Original Thrombolysis mean'] = \
        original_data[original_data['S2Thrombolysis'] == 1].mean()

    descriptive_stats['Synthetic Thrombolysis mean'] = \
        synth_df[synth_df['S2Thrombolysis'] == 1].mean()

    descriptive_stats['Original No thrombolysis mean'] = \
        original_data[original_data['S2Thrombolysis'] == 0].mean()

    descriptive_stats['Synthetic No thrombolysis mean'] = \
        synth_df[synth_df['S2Thrombolysis'] == 0].mean()

    descriptive_stats['Original Thrombolysis std'] = \
        original_data[original_data['S2Thrombolysis'] == 1].std()

    descriptive_stats['Synthetic Thrombolysis std'] = \
        synth_df[synth_df['S2Thrombolysis'] == 1].std()

    descriptive_stats['Original No thrombolysis std'] = \
        original_data[original_data['S2Thrombolysis'] == 0].std()

    descriptive_stats['Synthetic No thrombolysis std'] = \
        synth_df[synth_df['S2Thrombolysis'] == 0].std()
    
    descriptive_stats_all_runs.append(descriptive_stats)

colours = ['k', 'b', 'g', 'r', 'y', 'c', 'm']
fig = plt.figure(figsize=(10,10))
number_of_runs = 5 
# Note: Set x and y limits to avoid plotting values that are very close to zero

# Negative mean
ax1 = fig.add_subplot(221)
for run in range(number_of_runs):
    x = descriptive_stats_all_runs[run]['Original No thrombolysis mean'].copy()
    y = descriptive_stats_all_runs[run]['Synthetic No thrombolysis mean'].copy()
    x.drop(labels ='S2Thrombolysis', inplace=True)
    y.drop(labels ='S2Thrombolysis', inplace=True)
    colour = colours[run % 7] # Cycle through 7 colours
    ax1.scatter(x,y, color=colour, alpha=0.5)
ax1.set_xlabel('Original data')
ax1.set_ylabel('Synthetic data')
#ax1.set_xlim(1e-3, 1e2)
#ax1.set_ylim(1e-3, 1e2)
ax1.set_title('No thrombolysis mean')
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.grid()

# Positive mean
ax2 = fig.add_subplot(222)
for run in range(number_of_runs):
    x = descriptive_stats_all_runs[run]['Original Thrombolysis mean'].copy()
    y = descriptive_stats_all_runs[run]['Synthetic Thrombolysis mean'].copy()
    x.drop(labels ='S2Thrombolysis', inplace=True)
    y.drop(labels ='S2Thrombolysis', inplace=True)
    colour = colours[run % 7] # Cycle through 7 colours
    ax2.scatter(x,y, color=colour, alpha=0.5)
ax2.set_xlabel('Original data')
ax2.set_ylabel('Synthetic data')
ax2.set_title('Thrombolysis mean')
ax2.set_xlim(1e-3, 1.5e2)
ax2.set_ylim(1e-3, 1.5e2)
ax2.set_xscale('log')
ax2.set_yscale('log')
ax2.grid()

# Negative standard deviation
ax3 = fig.add_subplot(223)
for run in range(number_of_runs):
    x = descriptive_stats_all_runs[run]['Original No thrombolysis std'].copy()
    y = descriptive_stats_all_runs[run]['Synthetic No thrombolysis std'].copy()
    x.drop(labels ='S2Thrombolysis', inplace=True)
    y.drop(labels ='S2Thrombolysis', inplace=True)
    colour = colours[run % 7] # Cycle through 7 colours
    ax3.scatter(x,y, color=colour, alpha=0.5)
ax3.set_xlabel('Original data')
ax3.set_ylabel('Synthetic data')
ax3.set_title('No thrombolysis standard deviation')
ax3.set_xlim(1e-2, 1.5e3)
ax3.set_ylim(1e-2, 1.5e3)
ax3.set_xscale('log')
ax3.set_yscale('log')
ax3.grid()

# Positive standard deviation
ax4 = fig.add_subplot(224)
for run in range(number_of_runs):
    x = descriptive_stats_all_runs[run]['Original Thrombolysis std'].copy()
    y = descriptive_stats_all_runs[run]['Synthetic Thrombolysis std'].copy()
    x.drop(labels ='S2Thrombolysis', inplace=True)
    y.drop(labels ='S2Thrombolysis', inplace=True)
    colour = colours[run % 7] # Cycle through 7 colours
    ax4.scatter(x,y, color=colour, alpha=0.5)
ax4.set_xlabel('Original data')
ax4.set_ylabel('Synthetic data')
ax4.set_title('Thrombolysis standard deviation')
ax4.set_xlim(1e-2, 1e2)
ax4.set_ylim(1e-2, 1e2)
ax4.set_xscale('log')
ax4.set_yscale('log')
ax4.grid()

plt.tight_layout(pad=2)
plt.savefig('images/smote_correls.png', facecolor='w', dpi=300)
plt.show()

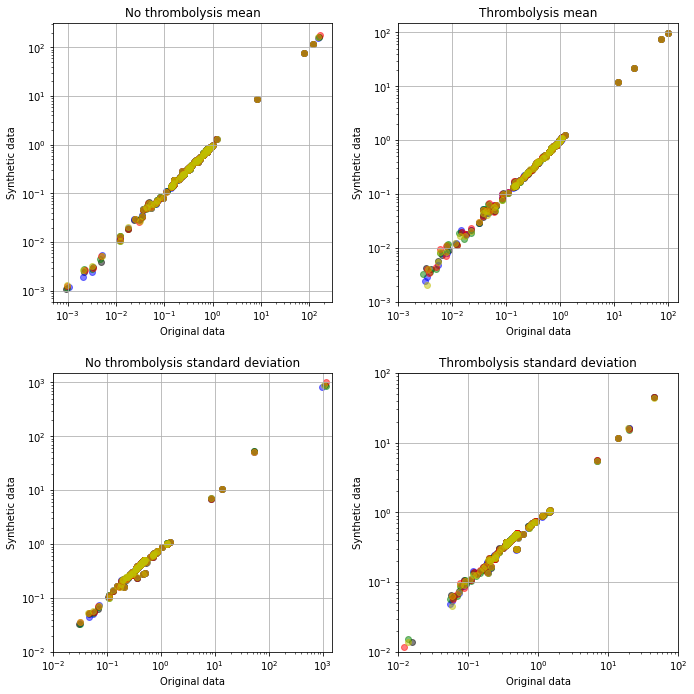
Feature means and standard deviations are well presevered in the synthetic (double SMOTE) data.