Stroke pathway timing distribution
Contents
Stroke pathway timing distribution#
Aims#
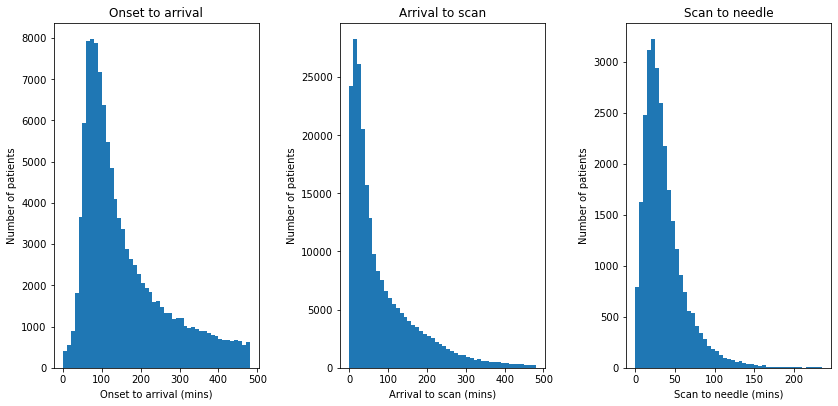
Visualise distributions of timings for:
Onset to arrival (when known)
Arrival to scan
Scan to needle
Find best distribution fit for the above.
Import libraries#
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats
from sklearn.preprocessing import StandardScaler
# Hide warnings to keep notebook tidy
import warnings
warnings.filterwarnings("ignore")
Import data#
# import data
raw_data = pd.read_csv(
'./../data/2019-11-04-HQIP303-Exeter_MA.csv', low_memory=False)
Plot distributions#
# Set up figure
fig = plt.figure(figsize=(12,6))
# Subplot 1: Histogram of onset to arrival
onset_to_arrival = raw_data['S1OnsetToArrival_min']
# Limit to arrivals within 8 hours
mask = onset_to_arrival <= 480
onset_to_arrival = onset_to_arrival[mask]
ax1 = fig.add_subplot(131)
bins = np.arange(0, 481, 10)
ax1.hist(onset_to_arrival, bins=bins, rwidth=1.0)
ax1.set_xlabel('Onset to arrival (mins)')
ax1.set_ylabel('Number of patients')
ax1.set_title('Onset to arrival')
# Subplot 2: Histogram of arrival to scan
arrival_to_scan = raw_data['S2BrainImagingTime_min']
# Limit to arrivals within 4 hours
mask = arrival_to_scan <= 480
arrival_to_scan = arrival_to_scan[mask]
ax2 = fig.add_subplot(132)
bins = np.arange(0, 481, 10)
ax2.hist(arrival_to_scan, bins=bins, rwidth=1)
ax2.set_xlabel('Arrival to scan (mins)')
ax2.set_ylabel('Number of patients')
ax2.set_title('Arrival to scan')
# Subplot 2: Histogram of scan to needle
scan_to_needle = \
raw_data['S2ThrombolysisTime_min'] - raw_data['S2BrainImagingTime_min']
ax3 = fig.add_subplot(133)
bins = np.arange(0, 240, 5)
ax3.hist(scan_to_needle, bins=bins, rwidth=1)
ax3.set_xlabel('Scan to needle (mins)')
ax3.set_ylabel('Number of patients')
ax3.set_title('Scan to needle')
# Save and show
plt.tight_layout(pad=2)
plt.savefig('output/pathway_distribution.jpg', dpi=300)
plt.show();
Fit distributions#
Distributions are fitted to bootstrapped 10k samples of the data.
Define function to fit distributions#
def fit_distributions(
data_to_fit, name, number_of_dist_to_plot=1, samples=10000):
# Reshape data and remove invalid values
yy = data_to_fit.values
mask = (yy > 0) & (yy < np.inf)
yy = yy[mask]
# Bootstrap sample
yy = np.random.choice(yy, samples, replace=True)
# Reshape
yy = yy.reshape (-1,1)
size = len(yy)
# Standardise data
sc = StandardScaler()
sc.fit(yy)
y_std = sc.transform(yy)
# Add +/- 0.0001 Std Dev jitter to avoid failure of fit for discrete data
jitter = np.random.uniform(-0.0001, 0.0001, samples)
jitter = jitter.reshape (-1,1)
y_std += jitter
# Test 10 distributions
dist_names = ['beta',
'expon',
'gamma',
'lognorm',
'norm',
'pearson3',
'triang',
'uniform',
'weibull_min',
'weibull_max']
# Set up empty lists to stroe results
chi_square = []
p_values = []
# Set up 50 bins for chi-square test
# Observed data will be approximately evenly distrubuted aross all bins
percentile_bins = np.linspace(0,100,51)
percentile_cutoffs = np.percentile(y_std, percentile_bins)
observed_frequency, bins = (np.histogram(y_std, bins=percentile_cutoffs))
cum_observed_frequency = np.cumsum(observed_frequency)
# Loop through candidate distributions
for distribution in dist_names:
# Set up distribution and get fitted distribution parameters
dist = getattr(scipy.stats, distribution)
param = dist.fit(y_std)
# Obtain the KS test P statistic, round it to 5 decimal places
p = scipy.stats.kstest(y_std, distribution, args=param)[1]
p = np.around(p, 5)
p_values.append(p)
# Get expected counts in percentile bins
# This is based on a 'cumulative distrubution function' (cdf)
cdf_fitted = dist.cdf(percentile_cutoffs, *param[:-2], loc=param[-2],
scale=param[-1])
expected_frequency = []
for bin in range(len(percentile_bins)-1):
expected_cdf_area = cdf_fitted[bin+1] - cdf_fitted[bin]
expected_frequency.append(expected_cdf_area)
# calculate chi-squared
expected_frequency = np.array(expected_frequency) * size
cum_expected_frequency = np.cumsum(expected_frequency)
ss = sum (((cum_expected_frequency - cum_observed_frequency) ** 2) /
cum_observed_frequency)
chi_square.append(ss)
# Collate results and sort by goodness of fit (best at top)
results = pd.DataFrame()
results['Distribution'] = dist_names
results['chi_square'] = chi_square
results['p_value'] = p_values
results.sort_values(['chi_square'], inplace=True)
# Report results
print ('\nDistributions sorted by goodness of fit:')
print ('----------------------------------------')
print (results)
print ()
# Plot
# ----
# Create figure
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
data = y_std.copy()
data = list(data.flatten())
data.sort()
# Get the top three distributions from the previous phase
dist_names = results['Distribution'].iloc[0:number_of_dist_to_plot]
# Histograms
# Divide the observed data into 100 bins for plotting (this can be changed)
number_of_bins = 100
bin_cutoffs = np.linspace(
np.percentile(data,0), np.percentile(data,99),number_of_bins)
h = ax1.hist(data, bins = bin_cutoffs, color='0.75')
x = h[1] # X values for hisotgram
for distribution in dist_names:
# Create an empty list to stroe fitted distribution parameters
parameters = []
# Set up distribution and store distribution paraemters
dist = getattr(scipy.stats, distribution)
param = dist.fit(data)
parameters.append(param)
# Get line for each distribution (and scale to match observed data)
pdf_fitted = dist.pdf(x, *param[:-2], loc=param[-2], scale=param[-1])
scale_pdf = np.trapz (h[0], h[1][:-1]) / np.trapz (pdf_fitted, x)
pdf_fitted *= scale_pdf
# Add a small amounbt of jitter to avoid overlying lines
jitter = np.random.uniform(0.99, 1.01, len(pdf_fitted))
pdf_fitted *= jitter
# Add the line to the plot
ax1.plot(x, pdf_fitted, label=distribution, alpha=1)
ax1.set_xlabel('Standardised value')
ax1.set_ylabel('Frequency')
ax1.set_title('Hisotgram of standardised values')
ax1.set_ylim(0, np.max(h[0]) * 1.05)
ax1.legend()
for distribution in dist_names:
# Set up distribution
dist = getattr(scipy.stats, distribution)
param = dist.fit(y_std)
# Get random numbers from distribution
norm = dist.rvs(*param[0:-2],loc=param[-2], scale=param[-1],size = size)
norm.sort()
# Calculate cumulative distributions
bins = np.percentile(norm,range(0,101))
data_counts, bins = np.histogram(data,bins)
norm_counts, bins = np.histogram(norm,bins)
cum_data = np.cumsum(data_counts)
cum_norm = np.cumsum(norm_counts)
cum_data = cum_data / max(cum_data)
cum_norm = cum_norm / max(cum_norm)
# plot observed and theoretical distributions
ax2.plot(cum_norm,cum_data,"o", label=distribution, alpha=0.5)
ax2.set_title('P-P plot')
ax2.set_xlabel('Theoretical cumulative distribution')
ax2.set_ylabel('Observed cumulative distribution')
ax2.legend()
ax2.plot([0,1],[0,1],'r--')
# Display plot
plt.tight_layout(pad=2)
plt.savefig(f'output/pp_{name}.jpg', dpi=300)
plt.show()
return
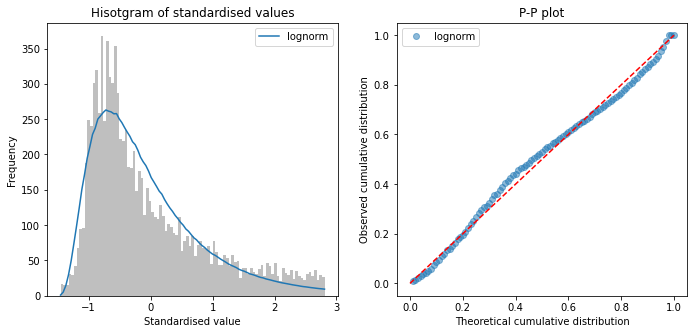
Fit distributions to onset-to-arrival#
onset_to_arrival = raw_data['S1OnsetToArrival_min']
# Censor at 8 hours
mask = onset_to_arrival <= 480
onset_to_arrival = onset_to_arrival[mask]
fit_distributions(onset_to_arrival, 'onset_to_arrival')
Distributions sorted by goodness of fit:
----------------------------------------
Distribution chi_square p_value
3 lognorm 913.458152 0.0
5 pearson3 2638.139962 0.0
2 gamma 2638.157425 0.0
9 weibull_max 4254.659947 0.0
8 weibull_min 5160.544206 0.0
6 triang 9114.152301 0.0
4 norm 18775.858420 0.0
7 uniform 38120.927402 0.0
1 expon 51718.034236 0.0
0 beta 64761.386652 0.0
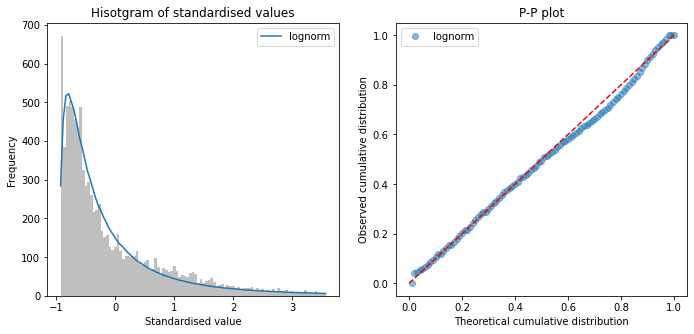
Fit distributions to arrival-to-scan#
arrival_to_scan = raw_data['S2BrainImagingTime_min']
# Censor at 8 hours
mask = arrival_to_scan <= 480
arrival_to_scan = arrival_to_scan[mask]
fit_distributions(arrival_to_scan, 'arrival_to_scan')
Distributions sorted by goodness of fit:
----------------------------------------
Distribution chi_square p_value
3 lognorm 1049.245175 0.0
8 weibull_min 2324.281283 0.0
1 expon 2359.439086 0.0
5 pearson3 3749.452982 0.0
2 gamma 3922.775328 0.0
0 beta 4652.542285 0.0
9 weibull_max 26233.976369 0.0
6 triang 56174.761885 0.0
4 norm 60651.483303 0.0
7 uniform 113031.621484 0.0
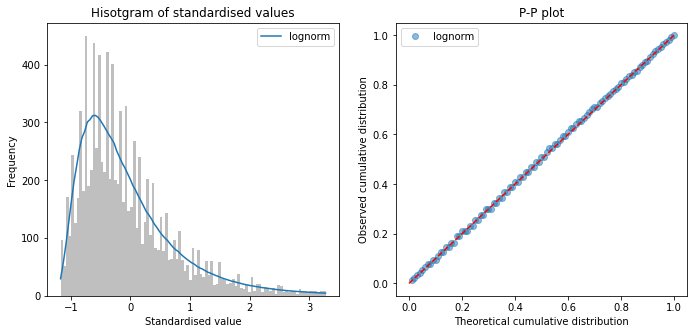
Fit distributions to scan-to-needle#
scan_to_needle = \
raw_data['S2ThrombolysisTime_min'] - raw_data['S2BrainImagingTime_min']
fit_distributions(scan_to_needle, 'scan_to_needle')
Distributions sorted by goodness of fit:
----------------------------------------
Distribution chi_square p_value
3 lognorm 96.655978 0.0
5 pearson3 556.709683 0.0
0 beta 649.232775 0.0
8 weibull_min 2155.745363 0.0
9 weibull_max 2794.257647 0.0
1 expon 21239.984412 0.0
4 norm 27519.140201 0.0
6 triang 154843.454429 0.0
7 uniform 195254.938614 0.0
2 gamma 659433.410326 0.0
Observations#
All timings show a right skew, with lognormal having minimum chi-squared
No distribution was a perfect fit to data (all had P<0.01)
Choose log normal distributions for pathway process times