Modelling the same patient population attending all hospitals

Aim:

• To predict the thrombolysis rate at each hospital if the same patient population (based on the national average patient characteristics) attend each hospital.

Patient population distributions are set to have the national average of:

• Arrival within 4 hours of stroke onset

• Proportion aged 80+

• Onset to arrival mean and standard deviation

The proportion of arrivals eligible for thrombolysis is set to the predicted 10k cohort rate for each hospital (adjusted to give thrombolysis use in those patients scanned within 4 hours of stroke onset).

The simulation model passes through 100 x 1k patient cohorts through each hospital model.

Load libraries

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import stats

Load data

# Scenario results
results = pd.read_csv('./output/scenario_results.csv')
# Pathway performance paramters used in scenarios
performance_base = pd.read_csv('./output/performance_base.csv')
performance_same_patients = \
    pd.read_csv('./output/same_patient_characteristics.csv')

performance_base

	stroke_team	thrombolysis_rate	admissions	80_plus	onset_known	known_arrival_within_4hrs	onset_arrival_mins_mu	onset_arrival_mins_sigma	scan_within_4_hrs	arrival_scan_arrival_mins_mu	arrival_scan_arrival_mins_sigma	onset_scan_4_hrs	eligable	scan_needle_mins_mu	scan_needle_mins_sigma
0	AGNOF1041H	0.154839	671.666667	0.425459	0.635236	0.681250	4.576874	0.557598	0.965596	1.665700	1.497966	0.935867	0.388325	3.669602	0.664462
1	AKCGO9726K	0.158892	1143.333333	0.395658	0.970845	0.428829	4.625486	0.597451	0.955882	2.834183	0.999719	0.908425	0.419355	2.904479	0.874818
2	AOBTM3098N	0.085885	500.666667	0.485470	0.619174	0.629032	4.603918	0.584882	0.935043	3.471419	1.254744	0.846435	0.267819	3.694918	0.518929
3	APXEE8191H	0.098634	439.333333	0.515679	0.716237	0.608051	4.590357	0.496452	0.966899	3.312930	0.714465	0.904505	0.258964	3.585094	0.751204
4	ATDID5461S	0.090689	275.666667	0.533546	0.573156	0.660338	4.427826	0.591373	0.878594	4.125690	0.549301	0.865455	0.315126	3.497262	0.608126
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
127	YPKYH1768F	0.105193	250.333333	0.321767	0.585885	0.720455	4.436404	0.569248	0.952681	3.779215	0.872809	0.844371	0.305882	3.982100	0.683223
128	YQMZV4284N	0.104186	358.333333	0.508511	0.945116	0.462598	4.664536	0.494740	0.948936	3.574735	0.912298	0.798206	0.308989	3.285165	0.463749
129	ZBVSO0975W	0.081602	449.333333	0.442130	0.465134	0.688995	4.562051	0.510524	0.972222	2.860226	0.990966	0.930952	0.273657	3.606046	0.575788
130	ZHCLE1578P	0.112647	796.000000	0.484694	0.733668	0.671233	4.606557	0.546648	0.949830	3.306916	0.842940	0.892569	0.262788	3.276043	0.795401
131	ZRRCV7012C	0.063058	597.333333	0.469504	0.779576	0.504653	4.636283	0.485394	0.977305	3.743456	0.662710	0.851959	0.189097	3.261270	0.803624

132 rows × 15 columns

Collate key results

Collate key results together in a DataFrame.

# Add admission numbers to results
admissions = performance_base[['stroke_team', 'admissions']]
results = results.merge(
    admissions, how='left', left_on='stroke_team', right_on='stroke_team')

# Calculate numbers thrombolysed
results['thrombolysed'] = \
    results['admissions'] * results['Percent_Thrombolysis_(mean)'] / 100

# Calculate additional good outcomes
results['add_good_outcomes'] = (results['admissions'] * 
    results['Additional_good_outcomes_per_1000_patients_(mean)'] / 1000)

# Get key results
key_results = pd.DataFrame()
key_results['stroke_team'] = results['stroke_team']
key_results['scenario'] = results['scenario']
key_results['admissions'] = results['admissions']
key_results['thrombolysis_rate'] = results['Percent_Thrombolysis_(mean)']
key_results['additional_good_outcomes_per_1000_patients'] = \
    results['Additional_good_outcomes_per_1000_patients_(mean)']
key_results['patients_receiving_thrombolysis'] = results['thrombolysed']
key_results['add_good_outcomes'] = results['add_good_outcomes']

key_results

	stroke_team	scenario	admissions	thrombolysis_rate	additional_good_outcomes_per_1000_patients	patients_receiving_thrombolysis	add_good_outcomes
0	AGNOF1041H	base	671.666667	15.20	12.76	102.093333	8.570467
1	AKCGO9726K	base	1143.333333	14.91	13.21	170.471000	15.103433
2	AOBTM3098N	base	500.666667	7.80	5.67	39.052000	2.838780
3	APXEE8191H	base	439.333333	10.40	7.59	45.690667	3.334540
4	ATDID5461S	base	275.666667	9.17	6.28	25.278633	1.731187
...	...	...	...	...	...	...	...
1183	YPKYH1768F	same_patient_characteristics	250.333333	7.47	4.98	18.699900	1.246660
1184	YQMZV4284N	same_patient_characteristics	358.333333	15.92	12.87	57.046667	4.611750
1185	ZBVSO0975W	same_patient_characteristics	449.333333	7.66	6.23	34.418933	2.799347
1186	ZHCLE1578P	same_patient_characteristics	796.000000	10.76	8.78	85.649600	6.988880
1187	ZRRCV7012C	same_patient_characteristics	597.333333	11.19	8.67	66.841600	5.178880

1188 rows × 7 columns

Summary stats

comparison = pd.DataFrame()
comparison['actual'] = key_results[key_results['scenario']=='base']['thrombolysis_rate'].values
comparison['cohort'] = key_results[key_results['scenario']=='same_patient_characteristics']['thrombolysis_rate'].values

comparison.describe().round(2)

	actual	cohort
count	132.00	132.00
mean	11.23	11.08
std	3.37	3.91
min	1.69	2.65
25%	9.24	8.29
50%	10.92	10.96
75%	13.12	12.87
max	24.23	24.93

Plot results

fig = plt.figure(figsize=(15,6))

ax1 = fig.add_subplot(131)
y = key_results[key_results['scenario']=='base']['thrombolysis_rate']
x = key_results[key_results['scenario']=='same_patient_characteristics']['thrombolysis_rate']
gradient, intercept, r_value, p_value, std_err = stats.linregress(x,y)
y_fit=intercept + (x*gradient)
ax1.plot(x, y, 'o', label='Data points')
ax1.plot(x, y_fit, 'r', label='Fitted regression')
ax1.plot([x.min(),x.max()],[x.min(),x.max()], 'b--', 
         label = 'Expected line if all variance\ndue to hospital processes')
mean_thrombolysis = comparison['actual'].mean()
ax1.plot([x.min(),x.max()],[mean_thrombolysis, mean_thrombolysis], 'g:', 
         label = 'Expected line if all variance\ndue to patient populations')

text='Slope: %.2f\nR-Squared: %.3f\nP value: %.3f' %(gradient,r_value**2,p_value)
ax1.set_xlim(0,26)
ax1.set_ylim(0,26)
ax1.text(17,2,text)
ax1.legend()
ax1.set_ylabel('Thrombolysis rate of 100k patient cohort')
ax1.set_xlabel('Actual thrombolysis rate')
ax1.set_title('Regression plot of actual vs cohort thrombolysis rate')

ax2 = fig.add_subplot(132)
zipped = zip(x,y)
for xx, yy in zipped:
    colour = 'red' if xx > yy else 'blue'
    ax2.plot([xx,xx], [xx,yy], 
             color=colour, lw=1, marker='o', alpha=0.6, markersize=4)
ax2.set_ylabel('Predicted thrombolysis rate of 100k patient cohort')
ax2.set_xlabel('Actual thrombolysis rate')
ax2.set_title('Scatter plot of actual vs cohort thrombolysis rate')
ax2.grid()


ax3 = fig.add_subplot(133)
bins = np.arange(1,25)
ax3.hist(y, bins = bins, color='k', linewidth=2,
           label='Cohort thrombolysis', histtype='step')
ax3.hist(x, bins = bins, color='0.7', linewidth=2,
           label='Actual thrombolysis', histtype='stepfilled')
ax3.set_xlabel('Thrombolysis rate (%)')
ax3.set_ylabel('Hospital count')
ax3.set_title('Histogram of actual vs cohort thrombolysis rates')
ax3.set_ylim(0,25)
ax3.legend()

plt.tight_layout(pad=2)
plt.savefig('./output/pathway_cohort.jpg', dpi=300)
plt.show()

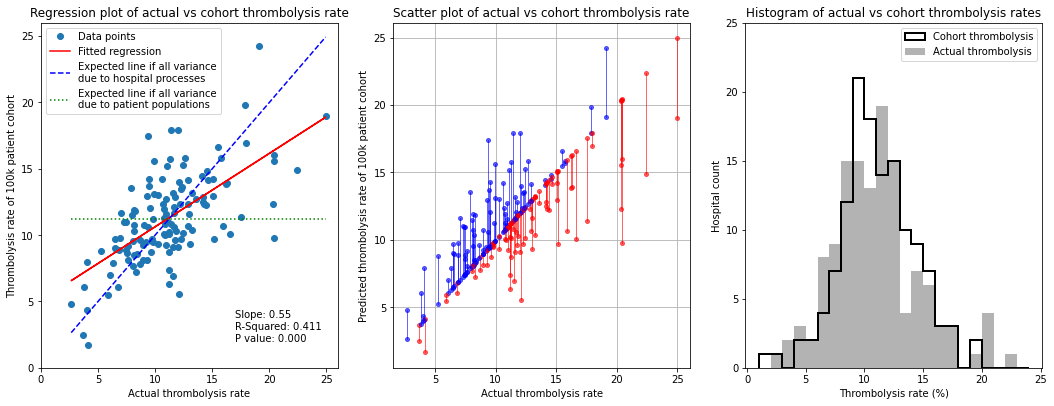
Observations

• In this experiment we fix the patient population, so that all hospitals in the model see the same patients, and pass those patients through each hospital model using that hospital’s pathway characteristics and decision model.

• When a standard (national average) patient population is passed through all hospitals the cohort thrombolysis rate at each hospital correlates with the actual thrombolysis use with R-square of 0.41, suggesting in-hospital processes and decision making account for about 40% of observed variance. Similarly, the regression fit between actual and cohort thrombolysis rate has a slope of 0.55, suggesting that 55% of the inter-hospital variance is due to hospital processes - when the patient population is unchanged there is, on average, a 0.55 percentage point difference in predicted cohort population thrombolysis rate for each 1 percentage point change in actual thrombolysis rate.

• As a general guide it seems that about half of the inter-hospital variance in thrombolysis rate is explained by in-hospital process and decisions, and the other half is explained by differences in local populations.

• As should be expected, the mean and distribution of the cohort thrombolysis use per hospital is very similar to the actual mean and distribution of thrombolysis use.

• There is a tendency for lower thrombolysing units to do better with a standard cohort, and those with higher thrombolysis rates to do worse. So there is a general observation that hospitals with high thrombolysis use do so partly because they have a more thrombolysable population, and vice versa.